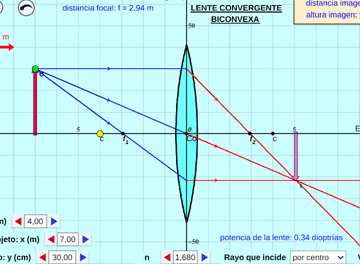
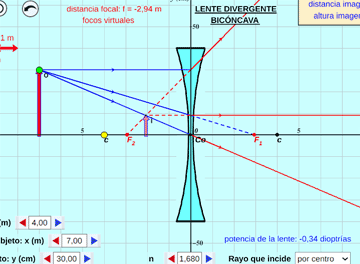
Se pueden ejecutar en cualquier navegador pues están codificados en el estándar de internet abierta (html5). Además los hemos optimizado para teléfonos inteligentes, aunque siempre es preferible abrirlos desde una computadora de escritorio, portátil o tablet para apreciar mejor todas sus características.
Durante 2025 continuaremos con la incorporación de estos novedosos medios tecnológicos a la enseñanza Preuniversitaria, tarea que se iniciara en 2007.
Simuladores de Matemática
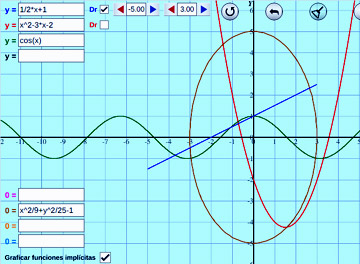
Graficador de funciones escalable:
Permite graficar hasta 8 funciones al mismo tiempo, incluidas funciones con dominios restringidos e implícitas
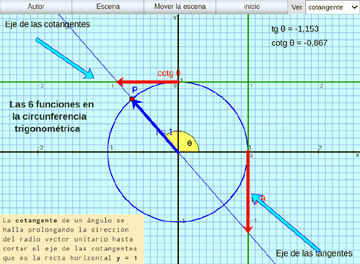
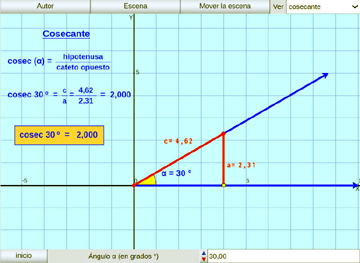
Circunferencia Trigonométrica:
Se presentan las seis funciones trigonométricas para ángulos de los cuatro cuadrantes
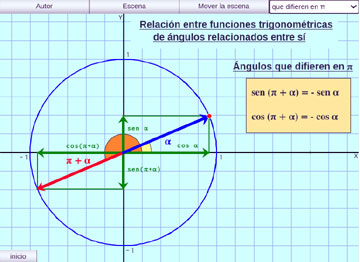
Ángulos relacionados entre sí:
Se muestra la relación entre funciones trigonométricas de ángulos relacionados entre sí
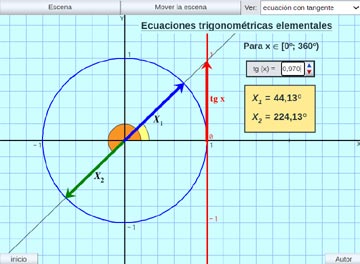
Ecuación trigonométrica elemental:
Se ilustran las soluciones de ecuaciones trigonométricas elementales
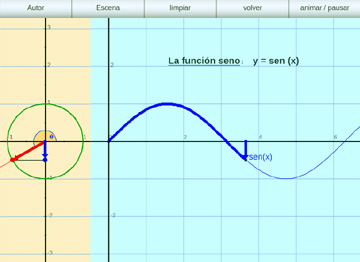
La gráfica de la función seno:
Se muestra la obtención de la gráfica de la función seno de x por proyección del radio unitario sobre el eje y
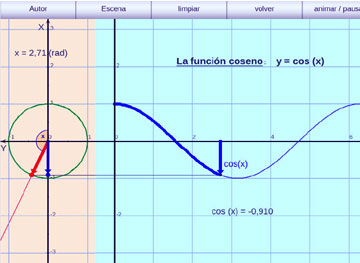
La gráfica de la función coseno:
Se muestra la obtención de la gráfica de la función coseno de x proyectando el radio unitario sobre el eje x
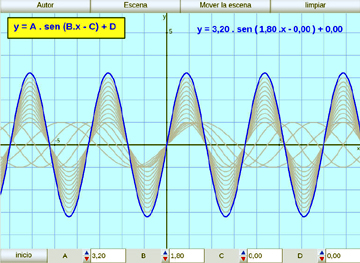
Estudio de la función seno:
Se estudian los parámetros de las sinusoides: amplitud, frecuencia y desplazamientos
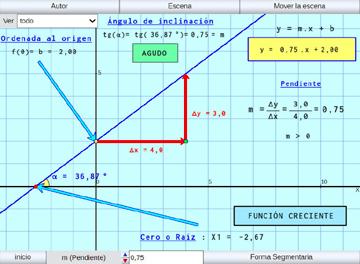
Función Afín o Lineal:
Se presenta la función lineal, y las características de su representación gráfica: la línea recta
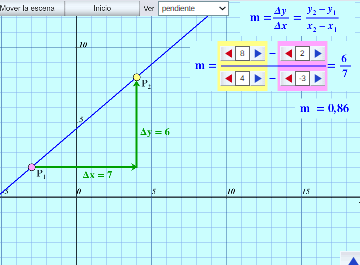
Rectas, pendiente y ecuaciones:
Se muestra la recta, el concepto de pendiente y las formas explícita y punto-pendiente
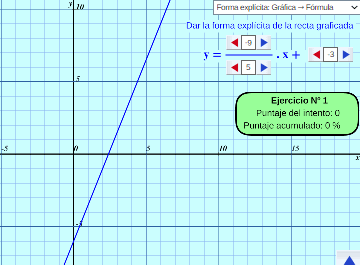
Rectas, gráficas y fórmulas (básico):
Se muestran 2 tipos de ejercicios distintos interactivos con función lineal y sus gráficas
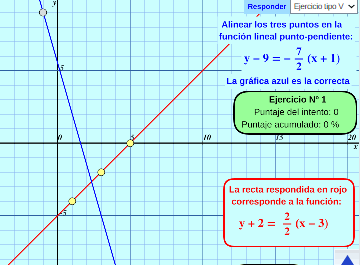
Rectas, gráficas y fórmulas (avanzado):
Se muestran 7 tipos de ejercicios distintos interactivos con función lineal y sus diversas formas
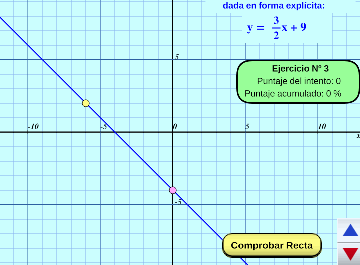
Rectas, evaluación (nivel básico):
Evaluación interactiva aleatoria con función lineal y sus gráficas. Ejercitación completa de 12 ejercicios
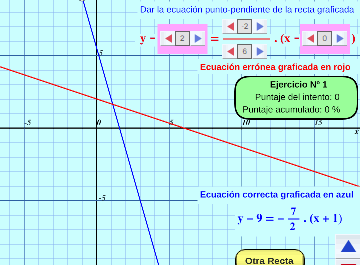
Rectas, evaluación (nivel avanzado):
Evaluación interactiva aleatoria con función lineal, sus distintas formas. Ejercitación completa de 50 ejercicios
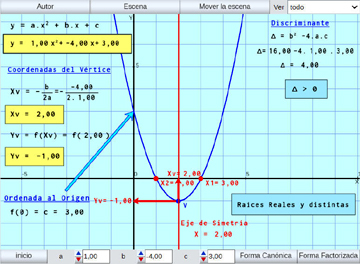
Función Cuadrática:
Se presenta la función cuadrática, y las características de su representación gráfica: la parábola
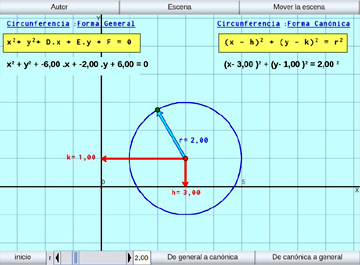
Circunferencia:
Se estudia la ecuación de la circunferencia en sus formas general y canónica, y pasajes entre ellas
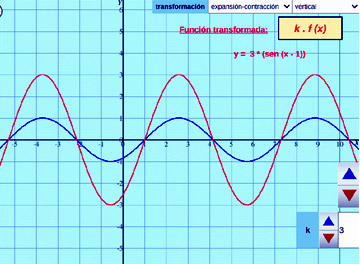
Transformación de Funciones:
Desplazamientos, reflexiones, expansiones y contracciones de las funciones al cambiar sus fórmulas
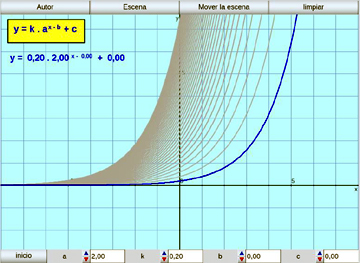
Función Exponencial:
Se muestra la función exponencial y los cuatro parámetros característicos que la definen
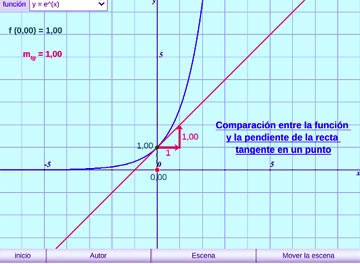
Función Exponencial de base e:
Se muestra una singularidad de la función exponencial de base e, la función es igual a su variación
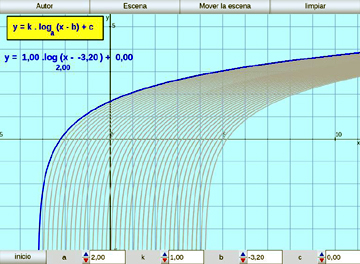
Función Logarítmica:
Se muestra la función logarítmica y los cinco parámetros característicos que la definen
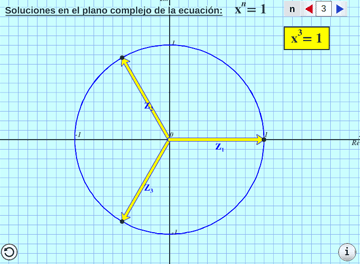
Raíces en el campo complejo:
Se muestran las soluciones en el campo complejo de una ecuación potencial básica
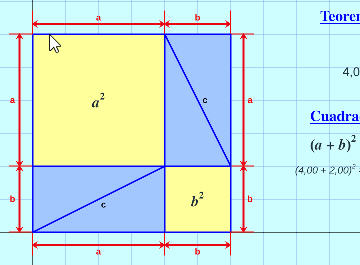
Teorema de Pitágoras:
Se demuestra en forma gráfica el teorema de Pitágoras moviendo y rotando triángulos rectángulos
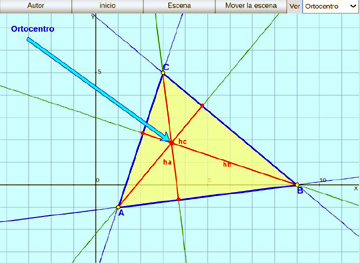
Alturas de un triángulo:
Se trazan las tres alturas de un triángulo y se observa su punto de intersección: el ortocentro
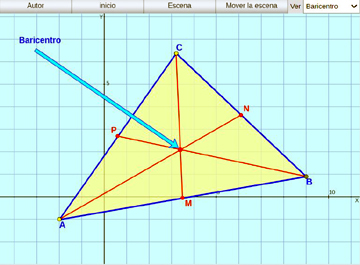
Medianas de un triángulo:
Se trazan las tres medianas de un triángulo y se observa su punto de intersección: el baricentro
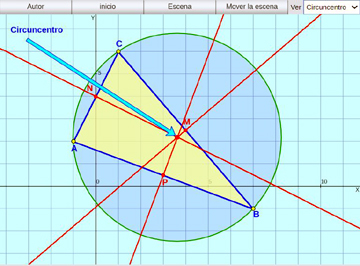
Mediatrices de un triángulo:
Se trazan las tres mediatrices de un triángulo y se observa su punto de intersección: el cincuncentro
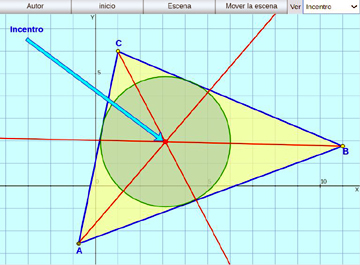
Bisectrices de un triángulo:
Se trazan las tres bisectrices de un triángulo y se observa su punto de intersección: el incentro
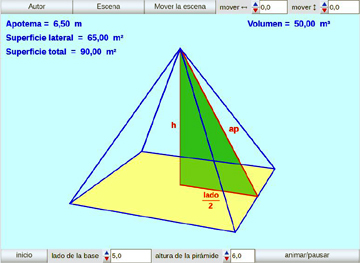
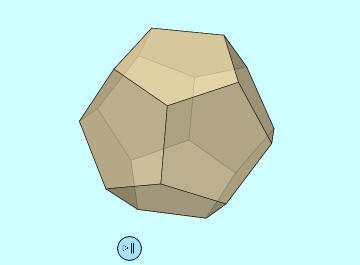
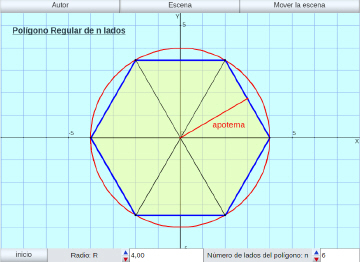
Pirámide en 3 dimensiones:
Se simulan en tres dimensiones la pirámide y la altura de sus caras triangulares: la apotema
Simuladores de Física
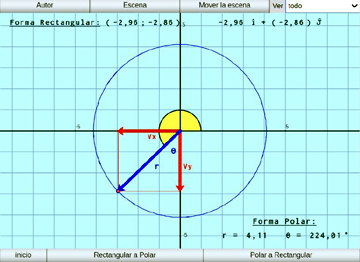
Vectores:
Se presenta el vector en el plano con sus dos formas de expresión: rectangular y polar, y pasaje entre ellas
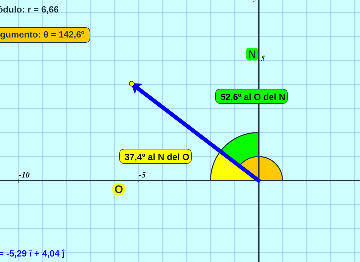
Vector con puntos cardinales:
Se mide el ángulo del vector con respecto a los puntos cardinales y se lo relaciona con el argumento
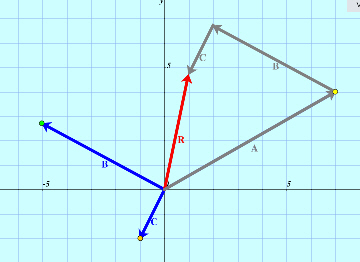
Álgebra de Vectores:
Suma de 2 o 3 vectores en el plano, resultante, se muestra la poligonal y se combinan linealmente dos vectores
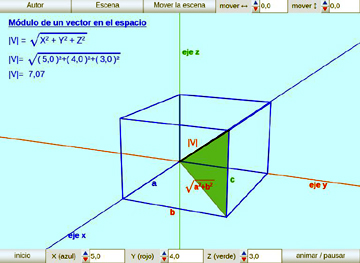
Pitágoras en 3 dimensiones:
Se presenta el vector en el espacio y la forma de hallar su módulo: el Teorema de Pitágoras en el espacio
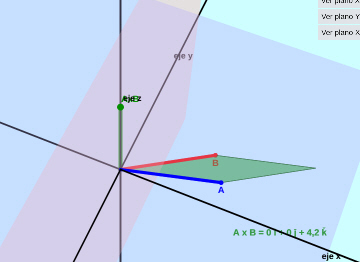
Producto entre Vectores:
Se presentan los productos entre vectores: el producto escalar (punto) y el producto vectorial (cruz) en R² y R³
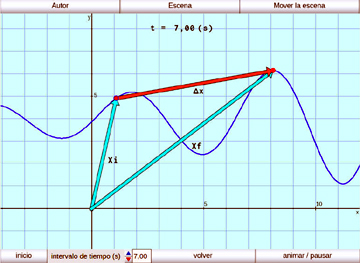
Desplazamiento:
Muestra el carácter vectorial de la posición y el desplazamiento en un movimiento bidimensional
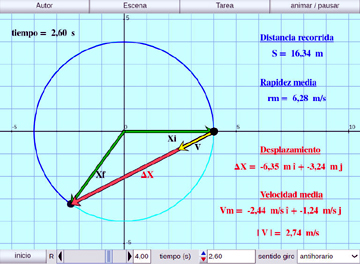
Velocidad y Rapidez:
Se estudia la diferencia conceptual entre velocidad (vector) y rapidez (escalar)
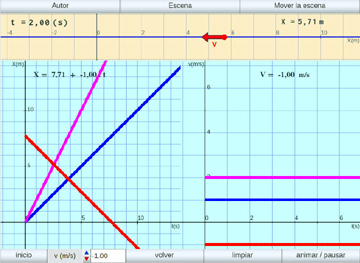
Movimiento Rectilíneo Uniforme:
Se muestra el movimiento en sí y las gráficas de la posición y velocidad en función del tiempo
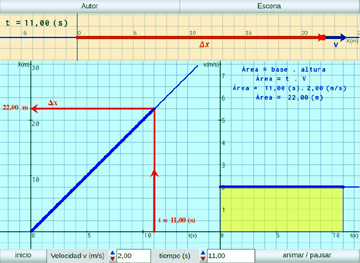
Área bajo v = f(t):
Se muestra que el desplazamiento de un móvil es el área debajo de la gráfica velocidad - tiempo
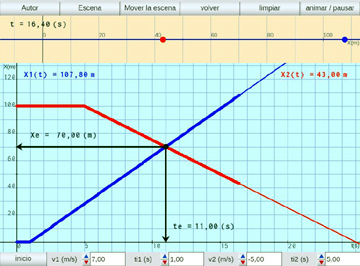
Encuentro de móviles con M.R.U.:
Se simulan problemas de encuentro de móviles que tienen movimientos rectilíneos uniformes
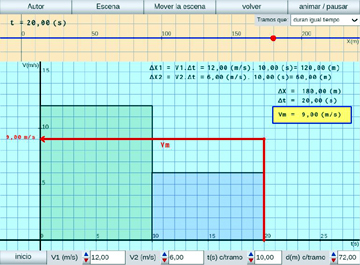
Dos M.R.U. sucesivos:
Se muestra cómo hallar velocidades medias de un móvil que tiene dos M.R.U. sucesivos.
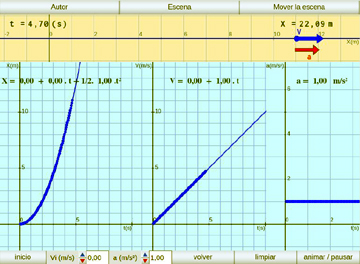
M. Rectilíneo Uniformemente Variado:
Se simula el movimiento M.R.U.V. y las gráficas de posición, velocidad y aceleración en función del tiempo
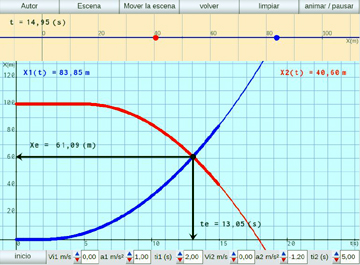
Encuentro de móviles con M.R.U.V.:
Se simulan problemas de encuentro de móviles que tienen movimiento rectilíneo uniformente variado
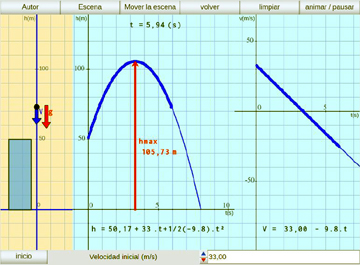
Caída Libre y Tiro Vertical:
Se simulan movimientos de caída libre, tiro vertical y otras variantes de movimientos verticales en el vacío
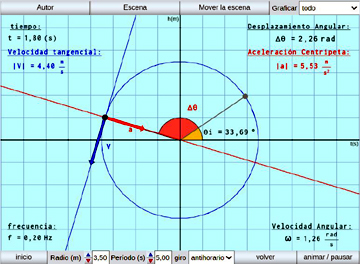
Movimiento Circular Uniforme (M.C.U.):
Se estudia el MCU y sus características: radio, período, velocidad angular, tangencial y aceleración centrípeta
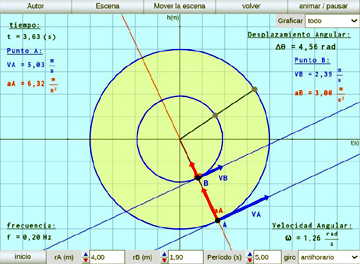
Movimiento en un disco con M.C.U.:
Se analizan las diferencias de velocidad tangencial y aceleración centrípeta de dos puntos sobre un disco
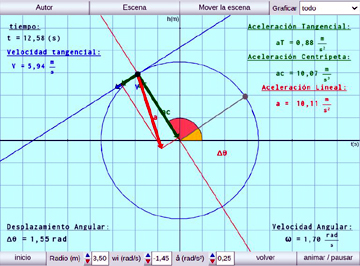
Mov. Circular Uniformemente Variado:
Se estudia el MCUV y sus características: velocidad angular y tangencial y las diversas aceleraciones
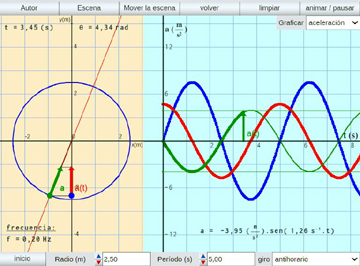
Movimiento Armónico Simple (M.A.S.):
Se simula el MAS como proyección de un MCU sobre un eje coordenado. Se ven las gráficas sinusoidales
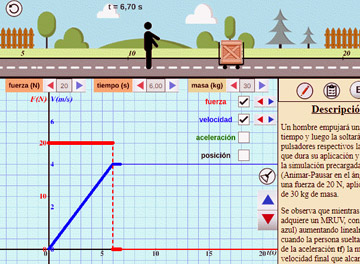
Dinámica, 2da Ley de Newton:
Se experimenta con masa y fuerza variable, se mide la aceleración y se comprueba la 2da Ley de Newton
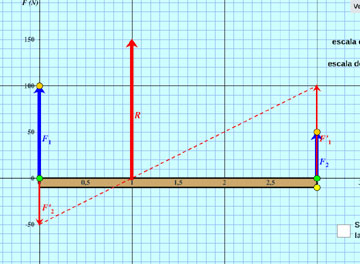
Composición de fuerzas paralelas:
Se muestra el proceso de construcción gráfico de la resultante de dos fuerzas paralelas. Resultante entre 3 paralelas
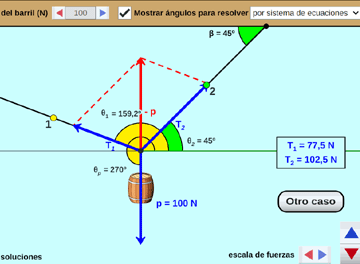
Cuerpo suspendido por cuerdas:
Se ilustra el equilibrio de un cuerpo suspendido por dos cuerdas, con las tensiones obtenidas gráficamente
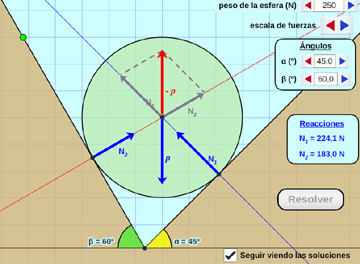
Esfera apoyada en dos planos:
Equilibrio de una esfera homogénea, con peso propio, apoyada en dos planos ideales sin rozamiento
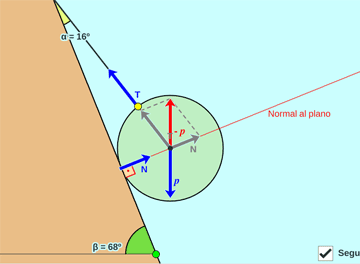
Esfera apoyada en un plano y cuerda:
Equilibrio de una esfera homogénea, con peso propio, apoyada en un plano y sostenida por una cuerda
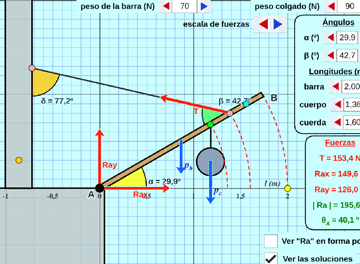
Barra articulada a pared y cuerda:
Equilibrio de barra articulada a una pared o al suelo y sostenida por una cuerda, con peso y otro colgando
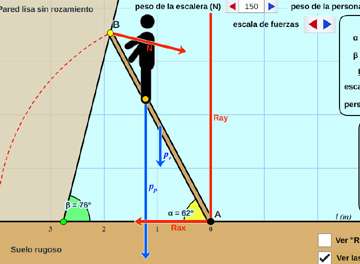
Escalera apoyada en pared ideal:
Equilibrio de una escalera apoyada en pared lisa sin rozamiento, con peso propio y persona subida
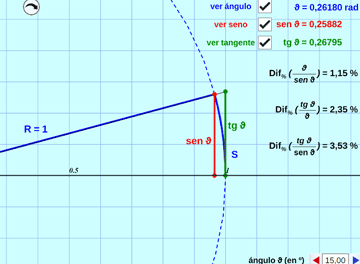
Aproximación paraxial:
Se justifica la apertura angular paraxial máxima válida para usar las fórmulas de la óptica en espejos y lentes
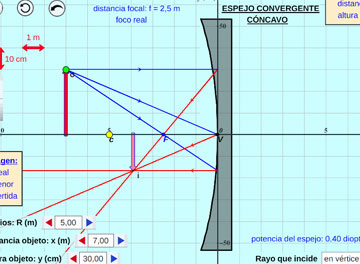
Imágenes en Espejos Cóncavos:
Se estudia la reflexión en espejos esféricos cóncavos formando imágenes virtuales y reales
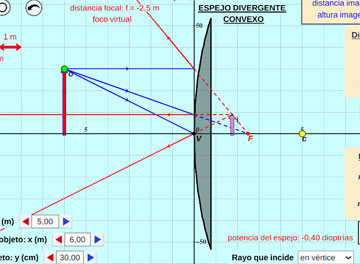
Imágenes en Espejos Convexos:
Se estudia la reflexión en espejos esféricos convexos formando imágenes siempre virtuales
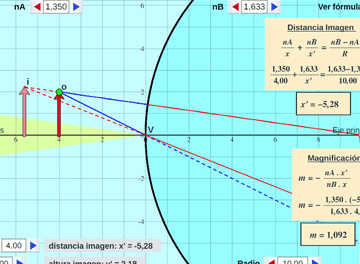
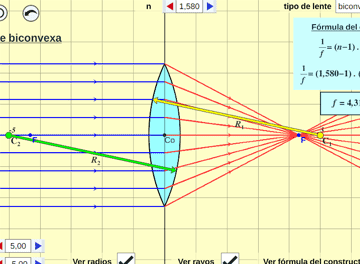
Imágenes en Dioptrios Esféricos:
Se estudia la refracción en dioptrios esféricos que separan medios de distinto índice de refracción